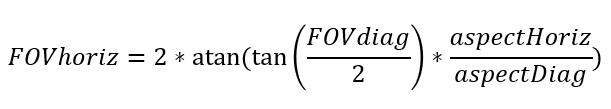I’ve spent more time figuring this stuff out. I’m sorry but this post is going to become complicated and is not intended for “light reading”. Here are my findings. I welcome any corrections or other insights.
The aspect ratio, while unit-less in measurements, are measured using linear quantities. When I use the term “linear” I don’t necessarily mean “in a straight line”. Instead, I am referring to a consistent unit of measure no matter where it occurs along a line.
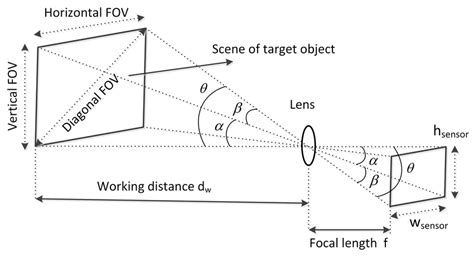
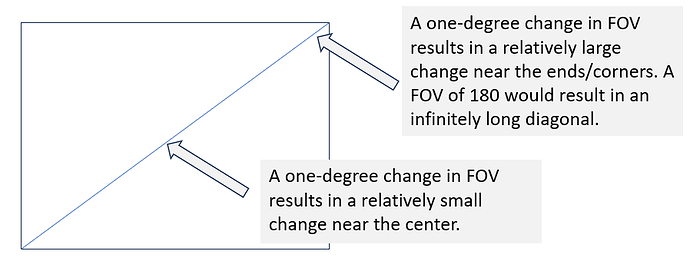
Field of view (FOV) is a linear measure but only in “degree space”. When the FOV is projected onto a flat surface, a linear change in the FOV degrees corresponds to a non-linear change when measured on that flat surface. Here is diagram to help describe this:
What this means is that one cannot use the Pythagorean Theorem to convert between the diagonal and horizontal FOV quantities because while the aspect ratio quantities of the sensor are linear, FOV values are not linear when projected onto that flat surface.
This concept is touched on in this description of the issue:
https://medium.com/insights-on-virtual-reality/converting-diagonal-field-of-view-and-aspect-ratio-to-horizontal-and-vertical-field-of-view-13bcc1d8600c
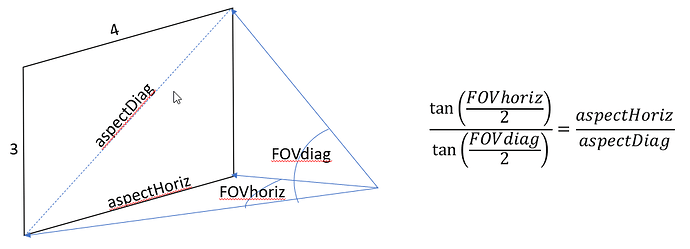
I have created this diagram to help describe how the ratio of tangents of the FOVs are equal to the ratios of horizontal to diagonal aspects. Remember, tangent is “opposite over adjacent” where, in this case, the “adjacent” length is the same for all aspect ratios and therefore not included in the equation.
Rearranging that equation to solve for FOVhoriz we get:
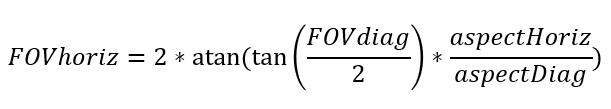
Using what I’ve learned, I have created a web application to compute the horizontal and vertical FOV values based on a 4x3 aspect ratio and a diagonal FOV. Using another rearrangement of the above equation I can compute the equivalent 16x9 diagonal FOV. Let me know if there is interest in this.
Using this application I have created a table comparing the FOV computations using the above equations to those using FOV values directly in the Pythagorean Theorem. You will notice that for small FOVs, there is not much difference between the two methods (which is expected). However, as the FOV becomes larger, the difference between the two methods becomes larger.
| FOVdiag |
FOVhoriz |
FOVvert |
FOVhoriz(linear) |
FOVvert(linear) |
| 20 |
16.1 |
12.1 |
16 |
12 |
| 30 |
24.2 |
18.3 |
24 |
18 |
| 40 |
32.5 |
24.6 |
32 |
24 |
| 50 |
40.9 |
31.3 |
40 |
30 |
| 60 |
49.6 |
38.2 |
48 |
36 |
| 70 |
58.5 |
45.6 |
56 |
42 |
| 80 |
67.7 |
53.4 |
64 |
48 |
| 90 |
77.3 |
61.9 |
72 |
54 |
| 100 |
87.3 |
71.1 |
80 |
60 |
|  |
|
|
|
Note: The last two columns in this table are those computed assuming FOV values can be used directly in the Pythagorean Theorem. As a result, these values are not correct but shown here for comparison purposes only.